CiRcuNfeRenCia!!

Circunferencia

De Wikipedia, la enciclopedia libre

Saltar a navegación, búsqueda

Una circunferencia es un conjunto de puntos del plano equidistantes de otro fijo, llamado centro; esta distancia se denomina radio. El segmento de recta formado por dos radios alineados se llama diámetro. Es la mayor distancia posible entre dos puntos que pertenezcan a la circunferencia. La longitud del diámetro es el doble de la longitud del radio. La circunferencia sólo posee longitud. Se distingue del círculo en que éste es el lugar geométrico de los puntos contenidos en una circunferencia determinada; es decir, la circunferencia es el perímetro del círculo cuya superficie contiene.

Puede ser considerada como una elipse de excentricidad nula, o una elipse cuyos semiejes son iguales. También se puede describir como la sección, perpendicular al eje, de una superficie cónica o cilíndrica, o como un polígono de infinitos lados, cuya apotema coincide con su radio.

La circunferencia de centro en el origen de coordenadas y radio 1 se denomina circunferencia unidad o circunferencia goniométrica .^{[1] [2] [3] [4] [5]}

Es una curva plana con infinitos ejes de simetría y sus aplicaciones son muy numerosas.

Contenido [ocultar] 1 Elementos de la circunferencia 2 Posiciones relativas 2.1 La circunferencia y un punto 2.2 La circunferencia y la recta 2.3 Dos circunferencias 3 Ángulos en una circunferencia 4 Longitud de la circunferencia 5 Ecuaciones de la circunferencia 5.1 Ecuación en coordenadas cartesianas 5.2 Ecuación vectorial de la circunferencia 5.3 Ecuación en coordenadas polares 5.4 Ecuación en coordenadas paramétricas 6 Área 7 Otras propiedades 8 Circunferencia en topología 9 Véase también 10 Referencias 11 Enlaces externos

 

[editar] Elementos de la circunferencia

Secantes, cuerdas y tangentes.

La mediatriz de una cuerda pasa por el centro de la circunferencia.

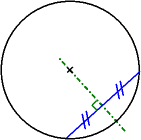
Existen varios puntos, rectas y segmentos, singulares en la circunferencia:

• centro, el punto interior equidistante de todos los puntos de la circunferencia;
• radio, el segmento que une el centro con un punto de la circunferencia;
• diámetro, el mayor segmento que une dos puntos de la circunferencia, y lógicamente, pasa por el centro;
• cuerda, el segmento que une dos puntos de la circunferencia; las cuerdas de longitud máxima son los diámetros;
• recta secante, la que corta a la circunferencia en dos puntos;
• recta tangente, la que toca a la circunferencia en un sólo punto;
  • punto de tangencia, el de contacto de la tangente con la circunferencia;
• arco, el segmento curvilíneo de puntos pertenecientes a la circunferencia;
• semicircunferencia, cada uno de los dos arcos delimitados por los extremos de un diámetro.

[editar] Posiciones relativas

[editar] La circunferencia y un punto

Un punto en el plano puede ser:

• Exterior a la circunferencia, si la distancia del centro al punto es mayor que la longitud del radio.
• Perteneciente a la circunferencia, si la distancia del centro al punto es igual a la longitud del radio.
• Interior a la circunferencia, si la distancia del centro al punto es menor a la longitud del radio.

[editar] La circunferencia y la recta

Una recta, respecto de una circunferencia, puede ser:

• Exterior, si no tienen ningún punto en común con ella y la distancia del centro a la recta es mayor que la longitud del radio.

• Tangente, si la toca en un punto (el punto de tangencia) y la distancia del centro a la recta es igual a la longitud del radio. Una recta tangente a una circunferencia es perpendicular al radio que une el punto de tangencia con el centro.

• Secante, si tiene dos puntos comunes, es decir, si la corta en dos puntos distintos y la distancia del centro a la recta es menor a la longitud del radio.

[editar] Dos circunferencias

Dos circunferencias, en función de sus pocisones relativas, se denominan:

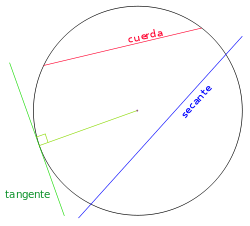
• Exteriores, si no tienen puntos comunes y la distancia que hay entre sus centros es mayor que la suma de sus radios. No importa que tengan igual o distinto radio. (Figura 1)

• Tangentes exteriormente, si tienen un punto común y todos los demás puntos de una son exteriores a la otra. La distancia que hay entre sus centros es igual a la suma de sus radios. No importa que tengan igual o distinto radio. (Figura 2)

• Secantes, si se cortan en dos puntos distintos y la distancia entre sus centros es menor a la suma de sus radios. No importa que tengan igual o distinto radio. Dos circunferencias distintas no pueden cortarse en más de dos puntos. Dos circunferencias son secantes ortogonalmente si el ángulo entre sus tangentes en los dos puntos de contacto es recto. (Figura 3)

• Tangentes interiormente, si tienen un punto común y todos los demás puntos de una de ellas son interiores a la otra exclusivamente. La distancia que hay entre sus centros es igual al valor absoluto de la diferencia de sus radios. Una de ellas tiene que tener mayor radio que la otra. (Figura 4)

• Interiores excéntricas, si no tienen ningún punto común y la distancia entre sus centros es mayor que 0 y menor que el valor absoluto de la diferencia de sus radios. Una de ellas tiene que tener mayor radio que la otra.

• Interiores concéntricas, si tienen el mismo centro (la distancia entre sus centros es 0) y distinto radio. Forman una figura conocida como corona circular o anillo. Una de ellas tiene que tener mayor radio que la otra. (Figura 5)

• Coincidentes, si tienen el mismo centro y el mismo radio. Si dos circunferencias tienen más de dos puntos comunes, necesariamente son circunferencias coincidentes.

[editar] Ángulos en una circunferencia

Ángulos en la circunferencia.

Arco capaz: los cuatro ángulos inscritos determinan el mismo arco y por tanto son iguales.

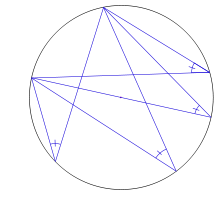
Un ángulo, respecto de una circunferencia, pueden ser:

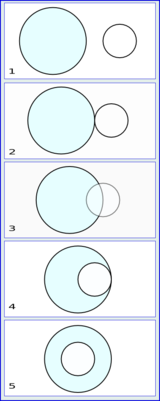
Ángulo central, si tiene su vértice en el centro de ésta. Sus lados contienen a dos radios.

La amplitud de un ángulo central es igual a la del arco que abarca.

Ángulo inscrito, si su vértice es un punto de la circunferencia y sus lados contienen dos cuerdas.

La amplitud de un ángulo inscrito en una circunferencia equivale a la mitad del ángulo central que delimita dicho arco. (Véase: arco capaz.)

Ángulo semi-inscrito, si su vértice es un punto de la circunferencia y sus lados contienen una cuerda y una recta tangente a la circunferencia. El vértice es el punto de tangencia.

La amplitud de un ángulo semi-inscrito es la mitad de la del arco que abarca.

Ángulo interior, si su vértice está en el interior de la circunferencia.

La amplitud de un ángulo interior es la mitad de la suma de dos medidas: la del arco que abarcan sus lados más la del arco que abarcan sus prolongaciones.

Ángulo exterior, si tiene su vértice en el exterior de la circunferencia

[editar] Longitud de la circunferencia

La longitud 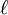de una circunferencia es:

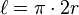
donde es la longitud del radio.

Pues 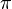(número pi), por definición, es el cociente entre la longitud de la circunferencia y el diámetro:

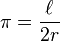
[editar] Ecuaciones de la circunferencia

[editar] Ecuación en coordenadas cartesianas

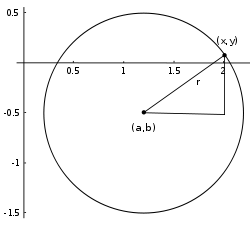
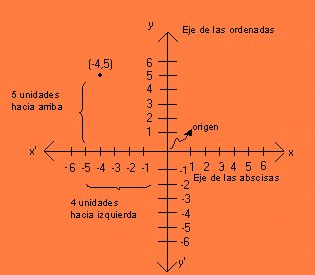
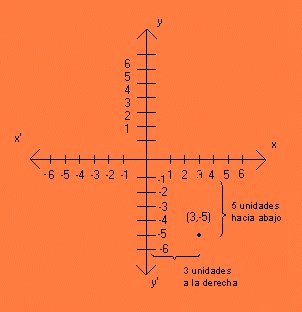
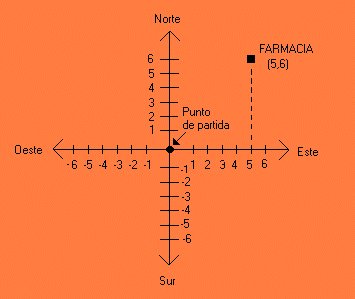
En un sistema de coordenadas cartesianas x-y, la circunferencia con centro en el punto (h, k) y radio r consta de todos los puntos (x, y) que satisfacen la ecuación

.

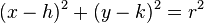Cuando el centro está en el origen (0, 0), la ecuación anterior se simplifica al

.

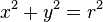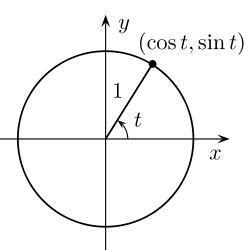
La circunferencia con centro en el origen y de radio la unidad, es llamada circunferencia goniométrica, circunferencia unidad o circunferencia unitaria.

De la ecuación general de una circunferencia,

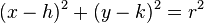
se deduce:

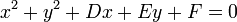
resultando:

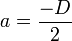
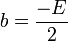
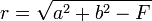
Si conocemos los puntos extremos de un diámetro: ,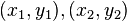

la ecuación de la circunferencia es:

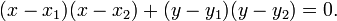
[editar] Ecuación vectorial de la circunferencia

La circunferencia con centro en el origen y radio R, tiene por ecuación vectorial: 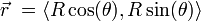.Donde 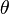es el parámetro de la curva, además cabe destacar que 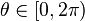. Se puede deducir fácilmente desde la ecuación cartesiana, ya que el componente X y el componente Y, al cuadrado y sumados deben dar por resultado el radio de la circunferencia al cuadrado. En el espacio esta misma ecuación da como resultado un cilindro, dejando el parámetro Z libre.

[editar] Ecuación en coordenadas polares

Cuando la circunferencia tiene centro en el origen y el radio es c, se describe en coordenadas polares como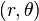

Cuando el centro no está en el origen, sino en el punto 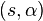y el radio es , la ecuación se transforma en:

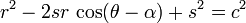
[editar] Ecuación en coordenadas paramétricas

La circunferencia con centro en (a, b) y radio c se parametriza con funciones trigonométricas como:

y con funciones racionales como

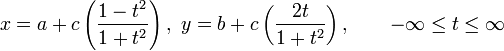
[editar] Área

Artículo principal: Área de un círculo

Área del círculo = π × área del cuadrado sombreado.

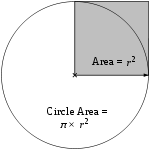
El área del círculo delimitado por la circunferencia es:

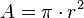
Esta última fórmula se deduce sabiendo que el área de cualquier polígono regular es igual al semiproducto entre el apotema y el perímetro del polígono, es decir: .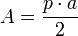

Considerando la circunferencia como el caso límite de un polígono regular de infinitos lados, entonces, el apotema coincide con el radio, y el perímetro con la longitud de la circunferencia, por tanto:

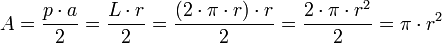
[editar] Otras propiedades

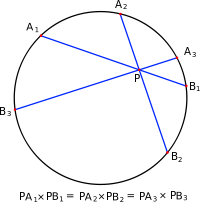
• Potencia de un punto: si dos cuerdas se intersecan, el producto de los segmentos formados en la una, es igual al producto de los segmentos formados en la otra cuerda, .

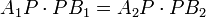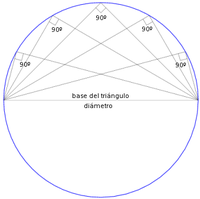
• El segundo teorema de Tales muestra que si los tres vértices de un triángulo están sobre una circunferencia dada, siendo uno de sus lados el diámetro de la circunferencia, entonces, el ángulo opuesto a éste lado es un ángulo recto (véase arco capaz).

Triángulos rectángulos inscritos en una semicircunferencia.

• Dados tres puntos cualesquiera no alineados, existe una única circunferencia que contiene a estos tres puntos (esta circunferencia estará circunscrita al triángulo definido por estos puntos). Dados tres puntos no alineados en el plano cartesiano 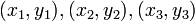, la ecuación de la circunferencia está dada de forma simple por la determinante matricial:

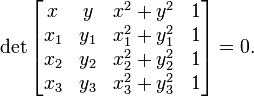
[editar] Circunferencia en topología

En topología, se denomina circunferencia a cualquier curva cerrada que sea homeomorfa a la circunferencia usual de la geometría (es decir, la esfera 1–dimensional). Se la puede definir como el espacio cociente determinado al identificar los dos extremos de un segmento cerrado.^[6]

Los geómetras llaman 3-esfera a la superficie de la esfera, mientras que topólogos se refieren a ella como 2-esfera y la indican como 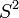.^[7]

Parábola (matemáticas)

Parábola (matemática)

De Wikipedia, la enciclopedia libre

Saltar a navegación, búsqueda

Para otros usos de este término, véase parábola.

Secciones cónicas.

La trayectoria de una pelota que rebota es una sucesión de parábolas.

En matemática, la parábola (del griego παραβολή) es la sección cónica resultante de cortar un cono recto con un plano paralelo a su generatriz.^[1]

Se define también como el lugar geométrico de los puntos que equidistan de una recta (eje o directriz) y un punto fijo llamado foco.

En geometría proyectiva, la parábola se define como la curva envolvente de las rectas que unen pares de puntos homólogos en una proyectividad semejante o semejanza.

La parábola aparece en muchas ramas de las ciencias aplicadas, debido a que las gráficas de ecuaciones cuadráticas son parábolas. Por ejemplo, la trayectoria ideal del movimiento de los cuerpos bajo la influencia de la gravedad.

Contenido [ocultar] 1 Historia 2 Propiedades geométricas 2.1 Lado recto 2.2 Semejanza de todas las parábolas 2.3 Tangentes a la parábola 3 Aplicaciones prácticas 4 Ecuaciones de la parábola 4.1 Ecuación involucrando la distancia focal 4.2 Ecuación general de una parábola 5 Referencias 6 Véase también 7 Enlaces externos

[editar] Historia

La tradición reza que las secciones cónicas fueron descubiertas por Menecmo en su estudio del problema de la duplicación del cubo,^[2] donde demuestra la existencia de una solución mediante el corte de una parábola con una hipérbola, lo cual es confirmado posteriormente por Proclo y Eratóstenes.^[3]

Sin embargo, el primero en usar el término parábola fue Apolonio de Perge en su tratado Cónicas,^[4] considerada obra cumbre sobre el tema de las matemáticas griegas, y donde se desarrolla el estudio de las tangentes a secciones cónicas.

Si un cono es cortado por un plano a través de su eje, y también es cortado por otro plano que corte la base del cono en una línea recta perpendicular a la base del triángulo axial, y si adicionalmente el diámetro de la sección es paralelo a un lado del triángulo axial, entonces cualquier línea recta que se dibuje desde la sección de un cono a su diámetro paralelo a la sección común del plano cortante y una de las bases del cono, será igual en cuadrado al rectángulo contenido por la línea recta cortada por ella en el diámetro que inicia del vértice de la sección y por otra línea recta que está en razón a la línea recta entre el ángulo del cono y el vértice de la sección que el cuadrado en la base del triángulo axial tiene al rectángulo contenido por los dos lados restantes del triángulo. Y tal sección será llamada una parábola

Apolonio de Perge

Es Apolonio quien menciona que un espejo parabólico refleja de forma paralela los rayos emitidos desde su foco, propiedad usada hoy en día en las antenas satelitales. La parábola también fue estudiada por Arquímedes, nuevamente en la búsqueda de una solución para un problema famoso: la cuadratura del círculo, dando como resultado el libro Sobre la cuadratura de la parábola.

[editar] Propiedades geométricas

Diferentes elementos de una parábola.

Diagrama que muestra la propiedad reflexiva, la directriz (verde), y las líneas que unen el foco y la directriz de la parábola (azul).

Aunque la definición original de la parábola es la relativa a la sección de un cono recto por un plano paralelo a su directriz, actualmente es más común definir la parábola como un lugar geométrico:

Una parábola es el lugar geométrico de los puntos equidistantes a una recta dada, llamada directriz, y a un punto fijo que se denomina foco.

De esta forma, una vez fija una recta y un punto se puede construir una parábola que los tenga por foco y directriz de acuerdo a la siguiente construcción. Sea T un punto cualquiera de la recta directriz. Se une con el foco dado F y a continuación se traza la mediatriz (o perpendicular por el punto medio) del segmento TF. La intersección de la mediatriz con la perpendicular por T a la directriz da como resultado un punto P que pertenece a la parábola. Repitiendo el proceso para diferentes puntos T se puede aproximar tantos puntos de la parábola como sea necesario.

De la construcción anterior se puede probar que la parábola es simétrica respecto a la línea perpendicular a la directriz y que pasa por el foco. Al punto de intersección de la parábola con tal línea (conocida como eje de la parábola) se le conoce como vértice de la parábola y es el punto cuya distancia a la directriz es mínima. La distancia entre el vértice y el foco se conoce como Distancia focal o Radio focal.

Los puntos de la parábola están a la misma distancia del foco F y de la recta directriz.

Construcción de puntos en una parábola.

[editar] Lado recto

El lado recto mide 4 veces la distancia focal

Al segmento de recta comprendido por la parábola, que pasa por el foco y es paralelo a la directriz, se le conoce como lado recto.

La longitud del lado recto es siempre 4 veces la distancia focal.

Siendo D, E los extremos del lado recto y T, U las respectivas proyecciones sobre la directriz, denotando por W la proyección del foco F sobre la directriz, se observa que FEUW y DFWT son cuadrados, y sus lados miden FW=2FV. Por tanto el segmento DE es igual a 4 veces el segmento FV (la distancia focal).

Las tangentes a la parábola que pasan por los extremos del lado recto forman ángulos de 45° con el mismo, consecuencia de que FEUW y DFWT sean cuadrados, junto con la construcción mencionada en la sección anterior. Además, tales tangentes se cortan en la directriz de forma perpendicular, precisamente en el punto de proyección W del foco, propiedades que pueden ser aprovechadas para construir una aproximación geométrica del foco y la directriz cuando éstos son desconocidos.

[editar] Semejanza de todas las parábolas

Todas las parábolas son semejantes, es únicamente la escala la que crea la apariencia de que tienen formas diferentes.

Dado que la parábola es una sección cónica, también puede describirse como la única sección cónica que tiene excentricidad e = 1. La unicidad se refiere a que todas las parábolas son semejantes, es decir, tienen la misma forma, salvo su escala.

Desafortunadamente, al estudiar analíticamente las parábolas (basándose en ecuaciones), se suele afirmar erróneamente que los parámetros de la ecuación cambian la forma de la parábola, haciéndola más ancha o estrecha. La verdad es que todas las parábolas tienen la misma forma, pero la escala (zoom) crea la ilusión de que hay parábolas de formas diferentes.

Un argumento geométrico informal es que al ser la directriz una recta infinita, al tomar cualquier punto y efectuar la construcción descrita arriba, se obtiene siempre la misma curva, salvo su escala, que depende de la distancia del punto a la directriz.

[editar] Tangentes a la parábola

La tangente bisecta el ángulo entre el foco, el punto de tangencia y su proyección.

Un resultado importante en relación a las tangentes de una parábola establece:

La tangente biseca el ángulo entre el foco, el punto de tangencia y su proyección.

En lo sucesivo, F denotará el foco de una parábola, P un punto de la misma y T su proyección sobre la directriz. Retomando la construcción dada para encontrar puntos de una parábola, sea MP la mediatriz del triángulo FPT, el cual es isósceles y por tanto biseca al ángulo FPT. Lo único que hay que verificar ahora es que MP también es la tangente en el punto P. Sea Q otro punto de la parábola y sea U su proyección en la directriz.

Puesto que FQ=QU y QU

¿Como graficar un plano cartesiano?

Para localizar puntos en el plano cartesiano se debe llevar a cabo el siguiente procedimiento:

1.Para localizar la abscisa o valor de x, se cuentan las unidades correspondientes hacia la derecha si son positivas o hacia a izquierda si son negativas, a partir del punto de origen, en este caso el cero.

2. Desde donde se localiza el valor de x, se cuentan las unidades correspondientes hacia arriba si son positivas o hacia abajo, si son negativas y de esta forma se localiza cualquier punto dadas sus coordenadas.

Ejemplos:

Localizar el punto A ( -4, 5 ) en el plano cartesiano. Este procedimiento también se emplea cuando se requiere determinar las coordenadas de cualquier punto que esté en el plano cartesiano.

 Determinar las coordenadas del punto M.

Las coordenadas del punto M son (3,-5).

 De lo anterior se concluye que:

Para determinar las coordenadas de un punto o localizarlo en el plano cartesiano, se encuentran unidades correspondientes en el eje de las x hacia la derecha o hacia la izquierda y luego las unidades del eje de las y hacia arriba o hacia abajo, según sean positivas o negativas, respectivamente.

    Doña Lupe  nos ha dicho que su farmacia  está dentro del centro de la ciudad . Supongamos que deseamos saber la ubicación  exacta de la farmacia de Doña Lupe Una vez  que ya estamos  en  el centro le preguntamos a un policía para que nos oriente. El policía nos ha dicho que caminemos 5 cuadras hacía el este y 6 cuadras hacía el norte para llegar a la farmacia.La cantidad de cuadras que tenemos que caminar  las podemos entender como coordenadas en un plano cartesiano.

Lo anterior lo podemos expresar en un plano cartesiano de la siguiente manera:

Para el problema planteado , el origen del plano será el punto de partida que es en donde le preguntamos al policía sobre la ubicación de la farmacia.

Funciones lineales:

Esta clase de funciones tienen dos características esenciales:

• Las variaciones entre dos valoresde la variable  independiente y la de sus correspondientes de la variable dependiente son uniformes.
• Todos los puntos de su gráfica están alineados.

Funciones de proporcionalidad directa:

Si en todos los pares de valores de una funciónde proporcionalidad directa dividimos la ordenada por la abscisa, obtenemos siempre el mismo número. Ese valor se llama constante de proporcionalidad, y se escribe habitualmente k.

Funciones de proporcionalidad inversa:

Si en todos los pares de valores de una función de proporcionalidad inversa multiplicamos la ordenada por la abscisa, obtenemos siempre el mismo número, que es la constante de proporcionalidad, y habitualmente se escribe k.

¿Qué es el plano cartesiano?

El plano cartesiano está formado por dos rectas numéricas, una horizontal y otra vertical que se cortan en un punto. La recta horizontal es llamada eje de las abscisas o de las equis (x), y la vertical, eje de las ordenadas o de las yes, (y); el punto donde se cortan recibe el nombre de origen.

El plano cartesiano tiene como finalidad describir la posición de puntos, los cuales se representan por sus coordenadas o pares ordenados. Las coordenadas se forman asociando un valordel eje de las "X" y uno de las "Y", respectivamente, esto indica que un punto se puede ubicar en el plano cartesiano con base en sus coordenadas, lo cual se representa como:

         P (x, y)

Se denominan coordenadas cartesianas en honor a René Descartes (1596-1650), el célebre filósofo y matemático francés que quiso fundamentar su pensamiento filosófico en la necesidad de tomar un «punto de partida» sobre el que edificar todo el conocimiento.

Como creador de la geometría analítica, Descartes también comenzó tomando un «punto de partida», el sistema de referencia cartesiano, para poder representar la geometría plana, que usa sólo dos rectas perpendiculares entre sí que se cortan en un punto denominado «origen de coordenadas», ideando las denominadas coordenadas cartesianas.

MaTeMaTiCaS III ( GeOgRaFiA aNaLiTiCa )

Se conoce como geometría analítica al estudio de ciertos objetos geométricos mediante técnicas básicas del análisis matemático y del álgebra en un determinado sistema de coordenadas. Se podría decir que es el desarrollo histórico que comienza con la geometría cartesiana y concluye con la aparición de la geometría diferencial con Carl Friedrich Gauss y más tarde con el desarrollo de la geometría algebraica.

Lo novedoso de la geometría analítica es que permite representar figuras geométricas mediante fórmulas del tipo f(x,y) = 0, donde f representa una función u otro tipo de expresión matemática.

En un sistema de coordenadas cartesianas, un punto del plano queda determinado por dos números, llamados abscisa y ordenada del punto. Mediante ese procedimiento a todo punto del plano corresponden siempre dos números reales ordenados (abscisa y ordenada), y recíprocamente, a un par ordenado de números corresponde un único punto del plano. Consecuentemente el sistema cartesiano establece una correspondencia biunívoca entre un concepto geométrico como es el de los puntos del plano y un concepto algebraico como son los pares ordenados de números. Esta correspondencia constituye el fundamento de la geometría analítica.

En un plano traza dos rectas orientadas perpendiculares entre sí (ejes) —que por convenio se trazan de manera que una de ellas sea horizontal y la otra vertical—, y cada punto del plano queda unívocamente determinado por las distancias de dicho punto a cada uno de los ejes, siempre y cuando se dé también un criterio para determinar sobre qué semiplano determinado por cada una de las rectas hay que tomar esa distancia, criterio que viene dado por un signo. Ese par de números, las coordenadas, quedará representado por un par ordenado (x,y), siendo x la distancia a uno de los ejes (por convenio será la distancia al eje vertical) e y la distancia al otro eje (al horizontal). 

Los razonamientos sobre la construcción de los ejes coordenados son igualmente válidos para un punto en el espacio y una terna ordenada de números, sin más que introducir una tercera recta perpendicular a los ejes X e Y: el eje Z.

Sin embargo no hay análogo al importantísimo concepto de pendiente de una recta. Una única ecuación lineal del tipo:

Representa en el espacio un plano. Si se pretende representar mediante ecuaciones una recta en el espacio tridimensional necesitaremos especificar, no una, sino dos ecuaciones lineales como las anteriores. De hecho toda recta se puede escribir como interesección de dos planos. Así una recta en el espacio podría quedar representada como:

Es importante notar que la representación anterior no es única, ya que una misma recta puede expresarse como la intersección de diferentes pares de planos.

Desde el punto de vista de la clasificación de Klein de las geometrías (el Programa de Erlangen), la geometría analítica no es una geometría propiamente dicha.

Desde el punto de vista didáctico, la geometría analítica resulta un puente indispensable entre la geometría euclidiana y otras ramas de la matemática y de la propia geometría, como son el propio análisis matemático, el álgebra lineal, la geometría afín, la geometría diferencial o la geometría algebraica.

Existe una cierta controversia sobre la verdadera paternidad de este método. Lo único cierto es que se publica por primera vez como "Geometría analítica", apéndice al Discurso del método, de Descartes, si bien se sabe que Pierre de Fermat conocía y utilizaba el método antes de su publicación por Descartes. Aunque Omar Khayyam ya en el siglo XI utilizara un método muy parecido para determinar ciertas intersecciones entre curvas, es imposible que alguno de los citados matemáticos franceses tuvieran acceso a su obra.

El nombre de geometría analítica corrió parejo al de geometría cartesiana, y ambos son indistinguibles. Hoy en día, paradójicamente, se prefiere denominar geometría cartesiana al apéndice del Discurso del método, mientras que se entiende que geometría analítica comprende no sólo a la geometría cartesiana (en el sentido que acabamos de citar, es decir, al texto apéndice del Discurso del método), sino también todo el desarrollo posterior de la geometría que se base en la construcción de ejes coordenados y la descripción de las figuras mediante funciones —algebraicas o no— hasta la aparición de la geometría diferencial de Gauss (decimos "paradójicamente" porque se usa precisamente el término "geometría cartesiana" para aquello que el propio Descartes bautizó como "geometría analítica"). El problema es que durante ese periodo no existe una diferencia clara entre geometría analítica y análisis matemático —esta falta de diferencia se debe precisamente a la identificación hecha en la época entre los conceptos de función y curva—, por lo que resulta a veces muy difícil intentar determinar si el estudio que se está realizando corresponde a una u otra rama.

La geometría diferencial de curvas sí que permite un estudio mediante un sistema de coordenadas, ya sea en el plano o en el espacio tridimensional. Pero en el estudio de las superficies, en general, aparecen serios obstáculos. Gauss salva dichos obstáculos creando la geometría diferencial, y marcando con ello el fin de la geometría analítica como disciplina. Es con el desarrollo de la geometría algebraica cuando se puede certificar totalmente la superación de la geometría analítica.

Es de puntualizar que la denominación de analítica dada a esta forma de estudiar la geometría provocó que la anterior manera de estudiarla (es decir, la manera axiomático-deductiva, sin la intervención de coordenadas) se terminara denominando, por oposición, geometría sintética, debido a la dualidad análisis-síntesis.

Actualmente el término geometría analítica sólo es usado en enseñanzas medias o en carreras técnicas en las que no se realiza un estudio profundo de la geometría.

 EsPeRo Y lEs GuStE!!!

Si No PuEs Ia K!!

Bienvenido

Ya tienes blog.

Para empezar a publicar artículos y administrar tu nueva bitácora:

1. busca el enlace Administrar en esta misma página.
   
2. Deberás introducir tu clave para poder acceder.

Una vez dentro podrás:

• editar los artículos y comentarios (menú Artículos);
  
• publicar un nuevo texto (Escribir nuevo);
  
• modificar la apariencia y configurar tu bitácora (Opciones);
  
• volver a esta página y ver el blog tal y como lo verían tus visitantes (Salir al blog).

Puedes eliminar este artículo (en Artículos > eliminar). ¡Que lo disfrutes!